What kind of energy is converted by our digestive system. How efficient is our digestive system compared to other living beings? Answer Below.
Answer to Q1: We can process some cooked foods better than most other organisms. However, this is a complex question, and there is no one simple answer. The short answer is that humans convert chemical energy through complex biological processes into heat and work (chemical-free energy becomes work). Our digestive systems, which convert what we eat into energy and other compounds, have evolved over time. In our digestive system, we break down complex molecules (food) into substances like sugar, which, when combined with oxygen, produces mass, heat, and work energy exchanges within our body. Work includes electrical work. An interesting take on our ability to eat processed foods is that somewhere during our evolution, we had to manage the energy demand to/and sustain the 84 Billion Neurons in our brains. Were it not for processed foods (think of them as predigested food) – perhaps we could not have developed our power of intelligence. Ask MHI about Optimized Entropic Pathways. Or check out why birds fly in formation.
What is an open system? A closed system is one in which no mass crosses the boundaries of your system. An isolated system is one in which no group or energy crosses the boundary. What is a steady-state system? Is a steady-state (time-invariant) energy conversion process reversible? Answer Below.
Answer to Q2: No. Steady-state Processes do not have to be reversible for open systems. An open system is a control volume where mass is input and/or output from the control volume as well as energy. When one imagines a system contained in a control volume that shows time-invariant properties, i.e., it is at a steady-state, new entropy can be continuously generated and dispersed through the boundaries of the control volume in a manner that ensures that other thermodynamic properties like Temperature, Pressure, Volume, Energy, and Entropy are measured to remain constant within the control volume. Such a process is, however, not a reversible process. Reversible implies that no new entropy is generated. A reversible process for an open system maximizes the work produced because it does not create new entropy. However, in reality, open systems are difficult to make fully reversible, although such an approximation is often used for solving engineering problems. Entropy is not a conserved property, unlike mass and energy, which are conserved properties (at least for velocities that do not approach the speed of light).
What if the device in Q2 was isentropic? Adiabatic? Answer Below.
Answer to Q3: For a reversible steady-state thermally isentropic cyclic process, the change in enthalpy is equal to the maximum work that can be extracted (or conversely, for a pump or refrigerator, it is the minimum work that is required to run the device for the objective necessary). The second Law sets the For a fluid exchanging energy in an open cyclic thermal device (bound by a control volume) and one which is adiabatic and has no changes to the control volume shape or size with time – one can obtain close to isentropic approximations but not always a strict steady-state condition when comparing the input and outlet thermodynamic properties of the fluid entering and leaving the device. Regardless, the Second Law sets the thermal efficiency limit and cannot be violated in any scenario.
Friction produces heat, and heat flow produces entropy. I understand this. But I have read that entropy is generated when two or more substances are mixed? Why? Answer Below.
Answer to Q4: The first entropy generation type is thermal entropy generation. Essentially the specific heat, after mixing, changes in comparison to the unmixed state (this can also be thought of in terms of the heat difference required for the new material from OK to the temperature of interest). A mixing process also creates new entropy by the generation of configurational entropy. Entropy generation is also used as a marker when shapes are created. Nature’s clever way of process-path and shape selection is called the MEPR principle. The acronym MEPR (sometimes MEPP) stands for ‘Maximum Entropy Production Rate,’ a principle that applies to self-organization even for avian flight formations.
Is there any theoretical limitation to wind energy conversion efficiency? Answer Below.
Answer to Q5: Yes, it is about 59.5%. The limit comes from the fact that air has to push through with a certain velocity to the other side of the windmill. Conserve momentum and mass.
Is there any theoretical limitation to solid-state solar energy conversion efficiency? Answer Below.
Answer to Q6: This is the most engaging of all the six questions. Although often cloaked in quantum terms, the issue lies in the second law of thermodynamics. The second law sets limits on maximum available work between two temperatures. Generally, the hotter a body becomes, the more heat it radiates. Simultaneously the peak radiation frequency downshifts. Power per unit volume is related to kT (see below). T is in Kelvin, kB=1.380 6488×10−23 J/K is the Boltzmann constant.
- Is there any apparent similarity between the relationship in the Euler characteristics of polyhedra and the Gibbs phase rule? Why do they appear to be so similar to non-dimensional quantities comprising the variable in the equations? Is there a topological connection? Answer: Euler Rule: Any convex polyhedron‘s surface has an Euler (Euler-Poincare) characteristic (E-V+2= F). Here V, E, and F are respectively the numbers of vertices (corners), edges, and faces in the given polyhedron. Gibbs Rule: If F is the number of degrees of freedom, C is the number of components, and P is the number of phases in thermodynamic equilibrium with each other, then the Gibbs Phase Rule applies to non-reactive multi-component heterogeneous systems in thermodynamic equilibrium. This is given by the equality (C-P+2= F), which looks very similar to the Euler rule. To answer the question of similarity, please do not hesitate to use the Borsuk-Ulam theorem (a remarkable topological theorem with symmetry implications). Regardless, it must be noted that there is no definite answer to this question yet. However, it does appear that the same stability principles that provide for an Euler Polyhedron appear to govern the stability principles for the phases of multicomponent chemical elements in equilibrium and could perhaps set the equilibrium conditions for the distribution of quarks in nucleons!
- Why is energy conserved? Answer: This is a consequence of Emmy Noether’s theorem on symmetry and the principle of least action. The principle of least action also appears to shed light on the postulate of shape selection (from https://arxiv.org/ftp/arxiv/papers/1605/1605.05005.pdf).
- Can Thermodynamics be used to infer beauty and its evolution? Answer: See clip on Beauty and Thermodynamics.
Temperature, EM spectrum, and other related concepts
For the explanation below, T is in Kelvin, kB=1.380 6488×10−23 J/K is the Boltzmann constant, and h is the Planck constant=6.62606957(29)×10−34J.s. A lower case c=299,792,458 m/s is the common symbol that is used to denote the velocity of e.m radiation (light). Lambda {![]() ) is the wavelength (m) and
) is the wavelength (m) and ![]() is the frequency (1/s).
is the frequency (1/s).
A famous equation called the Plancks equation shows that the power per unit volume is related to Temperature of a unit area of a surface The sun temperature is 5778K (see calculation below). This is only a modestly high temperature when compared to other more-active stars recognized in distant galaxies. The heat generated by the Sun is from nuclear fusion processes inside our Sun (yes a lot of entropy is also generated). The earth surface is at ~300K. The theoretical Carnot efficiency (this is the maximum allowed efficiency) between a source of heat at at a temperature Thot to a sink at a temperature Tcold is equal to (1-Thot/Td other similar concepts explained. cold). Therefore about 94.8% efficiency should be possible for converting to work from sunlight falling on earth. Unfortunately sunlight falls in a mid-range of the electromagnetic spectrum and has a wide variation of frequencies in the optical frequency range, from low frequency red region to the high frequencies like (blue – ultraviolet) region. Not all frequencies are easily absorbed by receptor materials (solar cells). There is thus an additional limit on the best possible direct work conversion from solar radiation. The best efficiencies reported so far for solar cells is about 44% with sunlight (not very close to the 94.8% mentioned above). The average amount of sunlight incident on earth is about 1300W/m2 . The sun may be considered to be a black-body. Radiance and spectral radiance are measures of the quantity of radiation that passes through or is emitted from a surface and falls within a given solid angle in a specified direction. The SI unit of radiance is watts per steradian per square metre (W·sr−1·m−2), while that of spectral radiance is W·sr−1·m−2·Hz−1 or W.·sr−1·m−3 depending on if the spectrum is a function of frequency or of wavelength. You may not have previously encountered the unit sr. It is the solid angle subtended at the center of a unit sphere by a unit area on its surface. Assume a sphere of radius r, any portion of its surface with area A = r2 will be one steradian. The surface area of a sphere is 4.pi.r2. This gives 4.pi = 12.56637 steradians The radiation spectrum and temperature relationships are discussed below. For a well-defined space that has equilibrium e.m radiation, i.e.a, wave that has an electric and magnetic field, the energy U is given by:
![]()
E is the electric field and B is the magnetic field. The SI unit for U is Joules.
From this equation and other laws of physics and statistics not described here, one may now derive the spectral energy densities as a function of frequency uv(T) or as a function of wavelength uλ(T):
where:
and L3 defines a volume.
Assume B is the spectral radiance with the units of W·sr−1·m−2·Hz−1. B is a function of frequency or wavelength and is given by the Plank expressions:
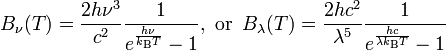
For radiation emitted by an ideal black body at temperature T, spectral radiance is described by Planck’s law formulation, while the integral of radiance over the hemisphere into which it radiates, in W/m2, is defined by the Stefan-Boltzmann law formulation.
Electric and magnetic fields store energy. In a vacuum, the (volumetric) energy density (in SI units) is given by
Planck’s law can also be written in terms of the spectral energy density (ui) by multiplying Bv by 4p/c:
Where V is volume.
The constant 4σ/c is called the radiation constant. Note that s (sigma) is the Stefan-Boltzmann constant. The energy density is related to a temperature corresponding to the equilibrium radiation.
Note that the energy density is related to both, i.e., the wave properties (frequency) and the temperature in the two expressions above. The energy density units are the same as pressure i.e. J/m3.
In the limit of low frequencies (i.e., long wavelengths), Planck’s law can be approximated as:
![]() or
or ![]()
In the limit of high frequencies (i.e., small wavelengths), Planck’s law can be approximated as
![]()
Wein’s displacement Law is a beneficial law emerging from the spectral density expression Wein’s displacement Law states that there is an inverse relationship between the wavelength of the peak of the emission of a black body ( ![]() max ) and its temperature (T).
max ) and its temperature (T).
 max. T= W-constant
max. T= W-constant
where λmax is the peak wavelength, T is the absolute temperature of the black body, and the W-constant in the equation above is called Wien’s displacement Law constant, which is equal to 2.8985×10−3 m·K = 2.8985 mm·K = 2,897,768.5 nm·K.
Sun Temperature: The sun may be considered to be a black body. The maximum (peak) emission wavelength of e.m. waves from the sun, peaks at a wavelength of ~501.5 nm (yellow). The sun’s surface temperature can be calculated from Wien’s displacement law which gives the temperature as equal to (2,897,768.5 nm·K/501.5nm) = 5778 K. Note: The sun’s surface is not uniform (the surface is all turbulent plasma) therefore this calculated temperature is an average based on the maximum emission wavelength observed. One may find other reported temperatures in the body of literature about the Sun’s temperature, but they will all be close to 5778K. Inside the sun i.e. close to its core, temperatures exceeding several million (close to 15 million) degrees Kelvin are expected that enable fusion of hydrogen into helium. For correctness one must note that helium and hydrogen both fuse in the core. The gamma rays generated from this fusion process take an enormous amount of time to finally transmit energy from the sun’s core to the surface’s surface. The range of frequencies emanating from the surface of the sun, that travel at the speed of light are not the same as those generated from the fusion process. Interaction with the dense mantle changes the range of frequencies that get transmitted. Some energy (a minimal amount) is also transferred into space by neutrinos that seemingly pass through the dense mantle of the sun without difficulty. Neutrinos travel also at speeds that approach the speed of light.
Human Body Energy Radiation and Temperature: On average, the human body radiates approximately ~100W. The normal human average temperature is 37C but varies with time of day and age. The thermometer measurement under the tongue correlates with the core body temperature. Variations exist for time of the day, age and perhaps also the gender as per some published studies. For thermal detection with imaging methods let us assume that a 32C-37C temperature is require to be detected. Application of Wien’s Displacement Law to the human body emission in such a range, results in a peak close to 9microns (micrometers). Consequently, any thermal imaging device developed for detecting humans should be constructed to be the most sensitive in the 6–15 micron wavelength range of detection. This wavelength range is beyond the visible spectrum (long IR range).
Bond Energy: Visible light is a small part of the entire electromagnetic spectrum (i.e. waves that have electric and corresponding magnetic fields). TAny electromagnetic wave velocity c (m/s) is the same in a vacuum for all frequencies and wavelengths. Is the frequency with units (1/s). The wavelength is given by c/ ![]() and because c is constant in any medium – the wavelength and frequency are inversely proportional. A higher peak frequency corresponds to higher temperature radiation. It can give much better Carnot efficiencies when converted to work (Rule: The best possible second law efficiencies come from the hottest possible source temperature for the same sink temperature). The frequency spectrum of sunlight corresponds to an average surface temperature of the sun of about ~5778K. One may note that the standard chemical bond energies correspond to energy levels in the e.m spectrum that are in the Infrared region of the e.m spectrum. From the two radiation laws above, we note that this corresponds to a temperature of about 1000-10000K. Nuclear bonds are stronger than chemical bonds with corresponding e.m. wave-energies that indicate the temperature to be in ~10000K-100000K range. Check out the e-ion ideation brochure to simulate some aspects of this answer.
and because c is constant in any medium – the wavelength and frequency are inversely proportional. A higher peak frequency corresponds to higher temperature radiation. It can give much better Carnot efficiencies when converted to work (Rule: The best possible second law efficiencies come from the hottest possible source temperature for the same sink temperature). The frequency spectrum of sunlight corresponds to an average surface temperature of the sun of about ~5778K. One may note that the standard chemical bond energies correspond to energy levels in the e.m spectrum that are in the Infrared region of the e.m spectrum. From the two radiation laws above, we note that this corresponds to a temperature of about 1000-10000K. Nuclear bonds are stronger than chemical bonds with corresponding e.m. wave-energies that indicate the temperature to be in ~10000K-100000K range. Check out the e-ion ideation brochure to simulate some aspects of this answer.
Standard Model of Matter: For the description of the structure of matter on the scale of elementary particles we use the Standard Model, which is a theoretical framework formulated back in the 1970’s. The particles considered as “elementary”, play various roles in the construction of matter. Bosons are carriers of forces: photons are related to electromagnetic interactions, eight types of gluons are responsible for strong interactions, and W+, W– and Z0 bosons mediate weak interactions. It is now imagined (and somewhat tested) that matter is formed by particles called fermions, divided into quarks and leptons. The standard Model has six types of quarks (down, up, strange, charm, top and bottom) and six types of leptons (electrons, muons, taons and their three corresponding neutrinos) as well as twelve antiparticles associated with them. The Higgs boson provides particles with mass (except to the gluons and photons).
IR Spectrum Devices: Somewhere in the range of 600C to 800C, the blackbody spectrum encroaches enough in the the visible to be seen as a dull red glow. At temperatures in the 50oC range (body to average room temperatures), almost all of the radiated energy from the body or wall is in the infrared part of the spectrum. The predominant wavelengths in this part of the spectrum are of (1000nm = 1 micron) and above. The lower the temperature, the peak shifts to a higher wavelength and as shown above could be mainly of the visible scale below 600oC. Thus the human body mostly loses radiation (heat) by emitting in the infra-red (IR) region, invisible to the eye. A typical human body controls its body temperature with a natural automatic regulation process and attempts to keep t around 37oC. An average human body emits about 100W of radiation at 37oC. This number increases with vigorous exercise. Detecting human body movement requires sparticularly sensitive sensors in the IR regions. Night vision goggles have thisfeature that accentuates IR and converts it to a visible frequency that the eye can detect. Almost all surface heating involves IR. Each quanta of IR has a lower frequency compared to UV. As the frequency increases towards UV radiation, the waves penetrate more as they have more energy. The energy of a photon depends on the wavelength. UV shades are recommended because UV has a shorter wavelength than IR. Note that the radiation power of a surface increases with temperature and with the emissivity in a non-linear manner. Note also the general trend of emissivity of materials is to increase as a function of temperature. However, emissivity and reflectance are not simple properties. Radiation is absorbed via mechanisms that involve allowed quantum states. The dielectric constant has a real and imaginary component and directly impacts reflectance. Therefore oddities are noted in reflectance measurements e.g. reflectance for a shiny metal can often decreases with peak temperature or increase (with wavelength). Emissivity is associated with high-temperature measurements (>300K) and reflectance with low (<300K) temperature measurements. Note that photons are not conserved.
Visible Spectrum Devices: Solar and UV panels can be of two types (1) those that absorb all radiation (black body) in the solar spectrum and (2) that selectively absorb to stimulate electron activity in semiconductors. These are classified as visible spectrum devices. Oxynitride, carbonitride, nitride and carbide coatings of transition metals and also of aluminium, titanium or zirconium made by the Cascade e-ion or D-e-ion devices often give antimicrobial properties. They are also used for wavelength-controlled surface devices for solar energy enhanced absorption (the MHI trade name is GoldenBlue(TM). MHI’s patented high emissivity and controlled boson, fermion, photon stimulators are the key to the next generation of power producing surfaces. See also deburr page for Golden/Blue surfaces/ microstructures for iron, zirconium, and titanium alloys. Surfaces can be manipulated to absorb some wavelengths and reflect others. As noted above, Kirchoffs law applies, however the amount transmitted or reflected at various wavelengths can be manipulated with transparent coatings e.g. of glass or gold plating or the more recently rediscovered copper-tin mirror materials. For example, a black body in the visible spectrum range can be covered with a layer (glass) that is transparent in the visible range but opaque in the UV or IR range. Such layering techniques are used for hot water solar heaters, for example.
In the visible spectrum, the units of lumens (amount of light in the visible range) and lux are used to calculate/infer the illumination, which usually pertains only to the visible spectrum objectives. Here, the device’s efficiency for providing illumination is defined by the luminous efficacy η in lumens per watt of the device (lm/W). The illuminance Ev in lux (lx) is equal to the power P in watts (W), multiplied by the luminous efficacy η, divided by the surface area A (m2): Ev(lx) = P(W) × η(lm/W) / A(m2). In terms of wavelength, the graphic below for the energy of the photon (shown in eV) would range from 720 microns to 390 microns (left to right).
Note that red is a higher wavelength radiation compared to violet.
Color: The reflection color from an object for sunlight depends on the intensity (including angle), polarization, photonic band gap, refractive index (real and imaginary parts), and other properties. The reflection or refraction of individual wavelengths is often not the same for all surfaces or thin films. Separation properties are utilized for thin-film devices. Thin films have many commercial applications, including partially transparent or anti-reflection coatings, mirrors, and optical filters. For graded and compositionally variant films, the colors yield considerable important information. Thin-film interference is a phenomenon associated with films that determine colors. Such interference partially explains the colors of nitrided surfaces, tempered colors, and the color of butterflies’ wings. The reflected, partially reflected, or refracted wave (depending on polarization) may interact and thus reveal information about the surface(s) from which individual frequency components are reflected, like the thickness of the film or the effective refractive index of the film medium.















