Review of Radiative Heating and Radiative Power

When an object is at a temperature above 0K (Zero Kelvin), it emits electromagnetic (em) radiation. The object has a natural glow with an intensity and type of radiation that depends on the temperature of the surface. Such emitted radiation can be thought to be wave-like with many frequencies, i.e., display a spectrum of wavelengths – same as velocity/frequency. The velocity of em radiation in a vacuum is fixed.  The radiation can also be thought of as comprising massless photons with a probability distribution of energy that depends on T, the temperature in Kelvin (more correctly, depends on kT where k is the Boltzmann constant).  Such a photon-based explanation of radiation is the more accepted theory of light/electromagnetic radiation, as it is the quantum-mechanical description of light.  According to our present understanding, the electromagnetic field itself is produced by photons, resulting in a local gauge symmetry and the laws of quantum field theory.  However, the wave-particle duality is not critical for heat transfer calculations because the experimental results follow Stefan-Boltzmann and Planck’s radiation laws discussed below.

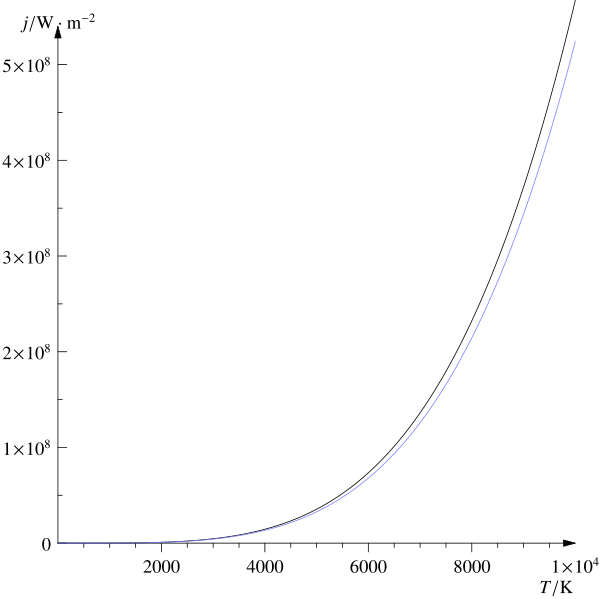
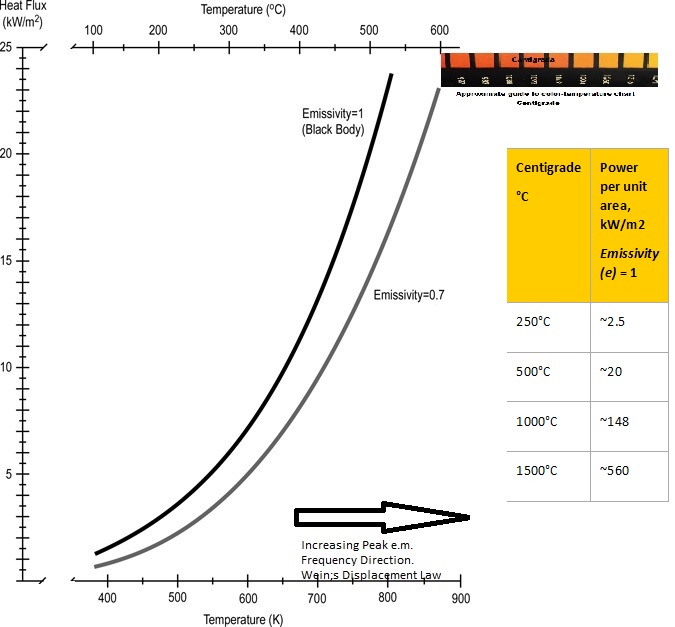
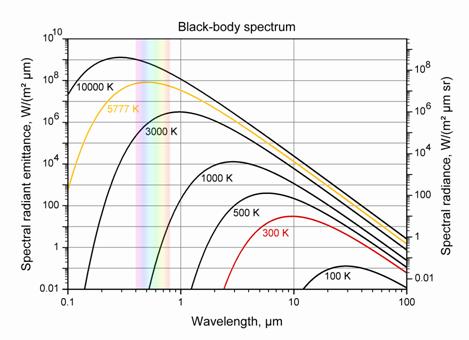
The Stefan-Boltzmann Law gives the maximum rate of radiation emitted (Power) by a surface with an area A, integrated over all wavelengths of the radiation.  Radiated Power Intensity, P (W) = e.s. A.Te^⁴  where e is the emissivity, Te is the temperature in Kelvin of the emitting surface, and s is the Stefan-Boltzmann Constant = 5.6703 x 10^-8 W/m²K⁴.  The emissivity (e) is a relatively complex variable encompassing several physics laws. The emissivity depends on temperature, wavelength, and the angle of emission. It is the ratio of power radiated by a material surface to the power radiated by a black body surface at the same temperature.   For a black body, e = 1.  The emissivity e ranges from 0-1 for solid materials.  Radiation can exert pressure – a simple way of thinking about this is that the rest-mass of photons is zero, but when they travel at the velocity of light – their effective mass is non-zero. Thus they have momentum and can exert force when encountering an obstruction.  The plot of radiation power per unit area as a function of temperature (the Stefan-Boltzmann law) is shown below.  A table that illustrates how steeply the total radiation power increases with the surface temperature of the emission surface is also shown.

Often continuous spectra are seen when free electrons change speed due to interaction with a potential and thus radiate photons with a continuous frequency spread. This is called Bremsstrahlung radiation. Further below, a discussion of the spectrum of wavelengths or the probability of a specific frequency range of photons emitted is presented (namely, Planck’s radiation law).

An important law called Kirchhoff’s law states that for material in thermal equilibrium, the emissivity e_l, at any given wavelength, and the absorptivity a_l at the same wavelength are equal (at a fixed surface temperature).  A black body is a perfect absorber as well as a perfect emitter. When radiation encounters an object, it may be absorbed, reflected, and refracted/transmitted.  For heat (infrared radiation), the transmission and refraction may only be through a few atomic layers where the energy is “absorbed.”  One may ignore transmission through more than a few atomic layers for such thermal (heat) radiation ( predominantly infrared IR spectrum comprising only of long wavelengths 1-100 micron range). Most solid bodies as they are are opaque to this radiation.

An object is called a black body if the following formula holds at all frequencies: a=e=1. What is commonly known as heat radiation lies in the Infrared part (the longer than light wavelengths).   It is a common assumption to consider the emissivity independent of wavelength to solve engineering problems related to heating by radiation.  Such an approximation is called the grey-body approximation.  Grey-body approximations are commonly made across the infrared (thermal radiation) spectrum.   The net power transfer P is described below in terms of the areas and temperatures of the absorbing and emitting surfaces.  The subscripts a and e stand for absorbing and emitting the surface of the radiation, respectively.  Pe and Pa are equal for a grey body in thermal equilibrium, and e = a.  The sun is a black body with e = 1 because it is very hot and dense at its core.  Although it is in equilibrium for all purposes (because of intense internal heating), it could have temperature variations, albeit slowly changing when measured over the surface.  Most materials found on earth are at a lower temperature, correspondingly with an absorptivity and emissivity below 1.  Note from the table above that the radiation power is magnified with an increase in the temperature, i.e., the radiative power follows a power law that is T⁴.  The net power transfer from a high-temperature surface to a lower-temperature surface by radiation is given by the Stefan-Boltzmann law:

s is the Stefan-Boltzmann Constant = 5.6703 x 10^-8 W/m²K⁴. When dealing with a problem like a sun radiating to the Earth for power calculations, note that there is only a section of the area of the sun that radiates to the Earth. The radiation is received over a specific section of the planet; -a larger area of the world radiates away from the Earth. (where h refers to the high-temperature emitting surface and, l refers to the lower temperature absorbing surface, A is the area). Note also that this law above is valid for most situations. However, the application to structures where features have less than the Wein wavelength -see below- could involve some correction terms.  Typically when in the room temperature range, this correction is for below ten micrometers, and at the MHI high-temperature device range, this is ~800nm.

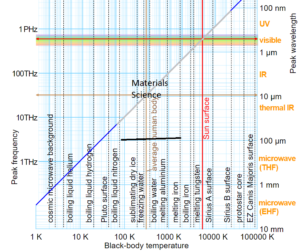
The spectrum of radiation in the electromagnetic spectrum is described in terms of its constituent frequency or wavelength of the radiation.   The total radiation a surface emits at a given temperature encompasses several wavelengths.  The temperature (T), peak wavelength (λ), and frequency (v) relationship is shown below.   Note that the visible spectrum region is only a tiny portion of the entire em spectrum.   Radiation from a body comprises multiple frequencies that may be considered to sum to a form of a resultant wave.  What is commonly known as heat radiation lies in the Infrared part (longer than light wavelengths).  Ultraviolet and X-Ray radiation is much higher frequency radiation (shorter wavelengths).  These are high-energy radiation and penetrate matter more than infrared radiation.   Note that the radiative power follows a power law that is T^{^4}.   Free radiating elements like Microheaters™, GlowPanels™, Thermoplates™, and,  Magnacoils™ are designed to maximize heat power output. On the other hand, a furnace with a closed chamber is optimized and designed for maximum temperature and low power loss (insulated).  When the transfer mechanism is convective, the best power transfer is achieved by Airtorch®.  A breakthrough device called the  Cascade e-ion may be employed when an extremely rapid power transfer is required.

The color of the planets:  Planet surfaces, or atmospheres, reflect and absorb sunlight.  The surface of Mercury is thought to be made up of igneous silicate rocks and dust.  Mercury has a dark gray, rocky surface with thick dust.  Venus is blanketed with a dense carbon dioxide atmosphere and sulphuric acid clouds that give it a light yellowish appearance.  Earth shows its blue oceans, white clouds, and green and brownish land.  Mars, covered with fine iron oxide, is red-orange.  Jupiter is a giant gas planet with an outer atmosphere, mostly hydrogen, and helium, with small amounts of water droplets, ice crystals, ammonia crystals, and other elements.  Clouds of these elements make shades of white, orange, brown, and red.  Saturn is also a giant gas planet with an outer atmosphere of mostly hydrogen and helium.  Its atmosphere has traces of ammonia, phosphine, water vapor, and hydrocarbons giving it a yellowish-brown color.  Uranus is a gas planet with methane gas mixed in with its mainly hydrogen and helium atmosphere.  This methane gas gives Uranus a greenish-blue hue.  Neptune also has some methane gas in its mostly hydrogen and helium atmosphere, giving it a bluish color.   Did you know plasmized gas has several tell-tale colors?

Radiation can also be considered comprising photons with a spectrum of energies (the wave and particle duality).  A photon is a fundamental particle that represents a quantum of electromagnetic radiation. The energy of an individual photon is higher for photons of a higher frequency.  It is only the particles that are bound in potentials that get quantized energies. Thus the photons that mediate transitions between these quantized energy states are quantized.  This explains why even though the Planck radiation equation is expressed as a continuous variable of wavelength, one notes that atoms’ emission and absorption spectra only yield discrete line signatures.  From solar cells to concrete testing to metal surface hardening, MHI devices utilize these differences in free electrons and bound electrons for useful device manipulation for specific applications. The effective mass from the famous equation  E=m.c^2 infers a vector momentum, which, when changed, gives rise to a vector force.  However, note that 1 J of energy is ~.11 x10^-16 Kg for em radiation.  Compare with 9.1 x 10^-31Kg as the mass of an electron at rest. So the photons can exert a punch on electrons as described by Ohio-born AH Compton (1892-1962) for inelastic scattering.

Planck’s energy law gives the relationship between energy and frequency for a Photon equation E = hν, where E is the energy per photon, ν is the frequency of the photon, and h is Planck’s constant equal to 6.626×10⁻³⁴ J.s.  When considering the wave-particle duality, the frequency of a wave is its rate of oscillation and is measured in Hertz, the SI unit of frequency, where one Hertz is equal to one oscillation per second.  A photon carries energy proportional to the ‘frequency‘ of the radiation (or inversely with the wavelength as the velocity is constant).   Photons belong to a  class of fundamental particles called bosons. Photons are the force carriers of the electromagnetic field.   Photons are not conserved.  Photons have a zero rest (invariant) mass.  The number of photons per second is related inversely to the electromagnetic/ light frequency (probability).   The photons/second = Pλ/hc = P/hν, where P is the Power in Watts, c is the speed of light, h is Planck’s constant, and ν is the frequency.  The energy E of a photon is given in electron volts.  Red light photons are about 1.7 eV, and blue light photons are about 3.2 eV (alternately, we could have said that the red light wavelength is about 0.8 microns and blue light is 0.3 microns).  Note that  1eV=1.60218e-19 Joules.

Note that the energy of a photon in eV (electron volts) is equal to 1.239/ (Wavelength in microns). 

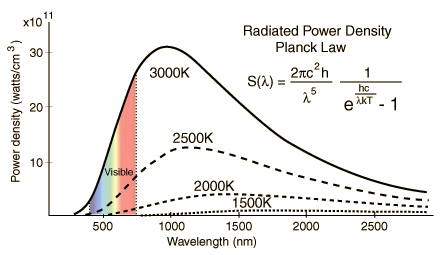
Planck’s Radiation Law gives the radiation power density as a function of wavelength and temperature for Black Bodies (shown in the plot(s) below) – also called the Planck formula.  S represents Radiation Power Density, W/m3 per steradian or Spectral Irradiance per steradian obtained from Planck’s  Radiation Law, a function of the wavelength.  Definition of Steridian:  An area on a sphere equal to the square of its radius, when observed from its center, is precisely one steradian.  This is similar to the relationship between arc length and the angle in radians in two dimensions.

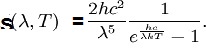
The radiated power density (S) as a function of wavelength is shown below for different temperatures. Planck’s constant h = 6.626×10−34 joule-second (J.s), and c is the velocity of electromagnetic radiation. Note that the power density increases with the temperature for any given wavelength. A peak (denoted as λmax) is also noted in the S vs. wavelength plot for any given temperature.  This peak shifts to a lower wavelength (higher frequency) with increased temperature. Wein’s radiation constant relates the peak wavelength and temperature.  The mathematical relationship is λmax. T = W, where W is a radiation constant, λmax is the peak wavelength, and T is the absolute temperature.  The radiation constant, W, is called Wien’s displacement constant equal to 2.8985×10−3 m·K.  The Planck equation (shown alongside the plots below) can be integrated over all wavelengths to yield the Stefan-Boltzmann law discussed above.  The units for the three graphs below should not be confused with the units of P (the total power given by the Stefan Boltzmann law). The radiation equation was originally derived semi-empirical before the quantum/statistical methods are discussed further below.

The power density S can also be derived by considering the radiation comprising photons.  When multiplied by frequency, Planck’s constant value, 6.626176 x 10^-34 J.s, is the smallest energy quanta that a corresponding photon can carry. From a knowledge of the gravitational constant, the Planck Energy based on the Planck Mass is M_pc² equal to 1.9561x 10^{^9} J.  Similarly, a Planck’s length ~1.6 x 10^-³⁵ m (the distance traveled by radiation during one Planck-time is one Planck-length) based on Planck’s time. ~5.39 x 10^-44 seconds. These are the smallest scale(s) in the universe (because of the Uncertainty Principle); however, the numbers are too small to measure directly or verify. Although not directly related to the uncertainty principle, those interested should also study Gödel’s incompleteness theorems on the limitations of possible knowledge of formal systems.

Planck’s radiation formula for photons is an example of the energy distribution predicted by Bose-Einstein statistics reflecting that the particles (photons) are indistinguishable and have integer spin. Two particles can be distinguished if their separation is significant compared to their de Broglie wavelength (λ=h/p, where p is the momentum for a massless photon, is E/c).  For air-gas molecules at STP (standard temperature and pressure), the molecules have a separation of 3 nm and de Broglie wavelengths of ~ 0.03nm, which is much smaller.  The kinetic energy is thus spread in a manner that reflects a Gaussian-type distribution of the kinetic energies of the gas atoms.  The mean energy in distribution is the measure of temperature.

On the other hand, electrons and photons are indistinguishable particles, but because of their quantum spin numbers may follow different energy distribution statistics, namely Fermi-Dirac statistics for electrons and Bose-Einstein statistics for photons.  For completeness, we should mention that lattice vibrations (phonons) are indistinguishable particles but may follow different statistics at different temperatures. At extremely low temperatures, even the larger particles (atoms) can have longer de Broglie wavelengths (i.e., as p (the momentum) tends to zero), and so especially when the atoms are highly concentrated and at a very low temperature, they can be considered as indistinguishable particles and ‘condense‘ into what is called zero-friction superfluids. One should note that “the standard model” that describes the make-up of all matter with numerous fundamental particles (even inside protons, neutrons, and other constituents) is now able to integrate almost all interactions of particle intensity probabilities – however, following  Planck’s law is OK for us for making thermal descriptions.  It does not matter which particles are being studied – nucleons or electrons- the quantum mechanical calculations can progress well within the Heisenberg Uncertainty Principle for making good predictions of forces and probability-polarity.  Regardless, experimental diffraction at tiny length scales is not yet available to properly validate these concepts.

The photon energy range with color in the visible region is shown below.

These graphs are reproduced from the open-source “Physics.”   Note that the energy of a photon in eV (electron volts) is equal to 1.239/ (Wavelength in microns).

Radiation interacts with chemical bonds. In the visible and UV regions, ionic dissociations (excited states) are feasible. The vibrational states are affected in the infrared region, as shown below.

Sun/Greenhouse effect:  The sun is a black body.  The greenhouse effect pertains to the earth receiving radiative energy with the distribution of wavelengths in the solar spectrum (from the sun, which has a surface temperature of ~5778K), but then emitting and reflecting a range associated with the much lower temperature of the earth (~ 300K).  The emission is mainly in the IR (infrared wavelengths).  Molecules absorb characteristic wavelengths.  Some of the emitted and reflected (polarized) radiation from the earth falls in the absorption band characteristics of CO2, water vapor, fluorocarbon, and gases in the air such as CH4, So2 NOx, and others, thus trapping a considerable part of the emitted and reflected IR radiation (heat). The interaction, whether elastic or inelastic, influences reflection and radiation. The sun may be considered to be a black body (e=1). In contrast, the earth may be regarded as a grey body (with e=0.8) for approximate energy distribution calculations. Note that only a grey body can reflect.

It should be noted that the emissivity of an object’s integrated emission is a temperature function.  For approximate energy calculations, it may be inferred that the Sun radiates 6.3 x 10^7 W/m2.  The earth (over the atmospheric area of the planet radius) receives ~1.3 x 10^3 W/m2 sunlight and radiates (from its actual surface) ~(250-350) W/m2, which is considerably absorbed by gasses in the atmosphere. The units of P in the equations above for power transfer between objects at two temperatures are W or W/m2, from the Stefan-Boltzmann law.  The units of power density above S are W/m3 or W/m3 per steradian (y-axis of the graphs above), i.e., from Planck’s Radiation Law formulation above.  The conversion between P and S at equilibrium involves Wein’s radiation constant or integration over the spectrum (all wavelengths) as described by Planck’s Law for the Energy of a Photon, namely that E = hν, where E is the energy per photon, ν is the frequency of the photon, and h is Planck’s constant equal to 6.626×10⁻³⁴ J.s. 

Shown below is the color spectrum of visible radiation and the energy associated with a particular wavelength of light. The solar spectrum credit is to https://en.wikipedia.org/wiki/File:Solar_Spectrum.png.  Note that O2, O3, and H2O absorption spectra are captured in the center graph. Still, it does not call out methane absorption, which is a minor constituent (because of low atmospheric concentration, 20-40 ppm level) but important when methane gas leaks are encountered (methane and other such gas lines (bands) absorb in the 1.62, 3.2 and 8.8-9.2 micron range).

Climate warming has led to the demand for deep decarbonization.  The major greenhouse gases are CO2, NOx, SO2, and CH4.  The last three are a much smaller component than carbon dioxide from fossil fuel combustion but more potent drivers of the greenhouse effect. Natural gas has considerable methane content, as does gas from biogenic sources.

Rapid industrial electrification of MW industrial heaters is most likely the fastest method to deep-decarbonize quickly.

Another reason for the warming is that ice (a solid) reflects a much more significant fraction of sunlight than water, reflecting only ~ 6% of the incident solar radiation. This happens because of the extinction coefficient and the refractive index differences between a liquid and a solid.  Sea ice is thus essential to prevent warming because it reflects sunlight (50-70%), thereby reducing the amount of energy absorbed at the surface. The change in the amount absorbed when there is less ice formation changes the water currents/circulation pattern.  An interesting observation is that snow (a semi-solid) can reflect ~90% of the incident solar radiation – even more than ice! This relates to surface roughness and correlation length differences when comparing snow and ice surfaces.  Any surface can be optimized for emission and reflection to improve the energy efficiency of the objective.

STEFAN-BOLTZMANN LAW: the units for P in the equations above for power transfer between objects at two temperatures are W or W/m2.  The power density units for S are W/m3 per steradian (y-axis of the two graphs above), i.e., from Planck’s Law.  Plancks Law describes that the conversion between P and S at equilibrium involves Wein’s radiation constant or integration over the spectrum (all wavelengths).    Wein’s law is the λmax = hc/zkT where z = 4.96511 (integration constant).   Here h is Planck’s constant, and k is the Boltzmann constant. Note also that pressure has units of J/m^3. So this radiation law also describes radiation pressure as a function of temperature and length scale, i.e., it can thus be thought to be analogous to an ‘ideal’ equation of state for radiation.

Link to review the use of the main spectral facility at Stanford University to measure the temperature dependence of absorption. Line broadening and emission transmission.  Link to the corresponding MHI furnace page.

The interaction of radiation with matter is quantized.  The range of photon energies in the IR spectrum has possibilities of interaction, as shown below with the vibrational state of molecules.  The UV-Vis spectrum of energies, i.e., the higher energy photons, can interact with more excited states of electrons in the atomic, molecular, and conduction bands.

IR Spectrum Devices

Somewhere in the range of 600C to 800C, the blackbody spectrum encroaches enough in the visible to be seen as a dull red glow.  At temperatures of ~50^oC, almost all of the radiated energy from the surface of a body or a wall lies in the infrared part of the spectrum (see above). The wavelengths in this part of the spectrum are of the order of (1000nm = 1 micron) and above. At low temperatures, the peak shifts to a higher wavelength and, as shown above, could be mainly of the visible scale below 600^oC.  Thus the human body mostly loses radiation (heat) by emitting in the infrared (IR) region, which is invisible to the eye.   A typical human body controls its temperature with a natural automatic regulation process and attempts to keep t around 37°C.   An average human body emits about 100W of radiation at 37^oC.  This number increases with vigorous exercise.

Detecting human body movement requires particularly sensitive sensors in the IR regions.   Night vision goggles have this feature that accentuates IR and converts it to a more visible frequency that the eye can detect.  Almost all surface heating involves IR. Each quantum of IR has a lower frequency compared to UV.  As the frequency increases towards UV radiation, the waves penetrate more as they have more energy.  The energy of a photon depends on the wavelength.  UV shades are recommended because UV has a shorter wavelength than IR.  Note that the radiation power of a surface increases with temperature and emissivity in a non-linear manner.  Note also that the general trend of emissivity of materials is to increase as a function of temperature.  However, emissivity and reflectance are not simple properties.  Radiation is absorbed via mechanisms that involve allowed quantum states. Emissivity is associated with high-temperature measurements (>300K) and reflectance with low (<300K) temperature measurements. The dielectric constant has a real and imaginary component and directly impacts reflectance (mainly from the real part). However, the refractive index and texture-caused dispersion are noted in reflectance measurements, e.g., the reflectance for a shiny metal can often decrease with peak temperature or increase because of plasmonic influence.

Visible Spectrum Devices

Solar and UV panels can be of two types (1) those that absorb all radiation (black body) in the solar spectrum, generally used for heating, and (2) that selectively absorb to stimulate electron activity in semiconductors.  These are classified as visible spectrum devices.  The cascade e-ion devices may combine the two types. The cascade e-ion is a device that can make oxynitride, carbonitride, nitride, and carbide surfaces/coatings of transition metals. Surfaces can be manipulated to absorb some wavelengths and reflect others. Such novel surfaces made by Cascade e-ion or D-e-ion devices also often impart antimicrobial properties.  MHI’s patented high emissivity and controlled boson, fermion, and photon stimulators are the keys to the next generation of power-producing surfaces.  See also deburr page for Golden/Blue surfaces/ microstructures for iron, zirconium, and titanium alloys.   As noted above, Kirchhoff’s law applies; however, the amount transmitted or reflected at various wavelengths can be manipulated with transparent coatings, e.g., glass or gold plating or the more recently rediscovered copper-tin mirror materials.  Variations in the types of surfaces enabled by the cascade e-ion are being discovered, e.g., a black body in the visible spectrum range can be covered with a layer (glass) that is transparent in the visible range but opaque in the UV or IR range. For example, hot water solar heaters may use such layering techniques.

How is light measured? What do Lumens and Lux signify?  What is Brilliance?

Brilliance in the context of light is related to the photons per second that our eyes sense.  In the visible spectrum, the units of lumens (amount of light in the visible range) and lux are used to calculate/infer the illumination, which usually pertains only to the visible spectrum objectives. Lumens are computed by knowing the spectrum or number of photons per second in the “light” frequencies and converting it to an absolute number slightly roundaboutly.  The luminous efficacy η defines the device’s efficiency for providing illumination in lumens per watt of the device (lm/W).  The illuminance E_v in lux (lx) is equal to the power P in watts (W), multiplied by the luminous efficacy η, divided by the surface area A (m²):  E_v(lx) = P_(W) × η_(lm/W) / A_(m2₎.   Note that red is a higher wavelength radiation compared to violet.  In terms of wavelength, the graphics above and below for the energy of the photon (shown in eV) would range from 720 microns to 390 microns (left to right). The power of radiation given in photons per second and the lumens are related to brightness by the number of photons per second in the visible range.

Luminous intensity is the perceived power per unit solid angle. Luminous intensity should not be confused with luminous flux, the total perceived power emitted in all directions. If a lamp has a 1-lumen bulb and the optics of the lamp are set up to focus the light evenly into a 1-steradian beam, then the beam would have a luminous intensity of 1 candela.  The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540×1012 hertz (green) and that has a radiant intensity in that direction of 1/683 watt per steradian.

Different light emitters can now be compared – an LED source gives 90 lumens per Watt compared to an incandescent bulb which is about 30 lumens per watt. Theoretically, the best estimate is that one watt of power in the ~540 nm wavelength range can result in ~680 lumens (lm).   The good news is that every year appears to bring a cost reduction with an increase in lumens/watt/device – a twenty-year trend.

As described above, Lux is a measure of lumens’ flux per unit area.  Remember, we have loosely used the word brightness above as it depends on the eye and other aspects of roughness and color, i.e., on the number of photons per second we can observe.

A few rules of reflection intensity

Although the primary law of reflection states that the angle of incidence and reflection are equal, one can understand that the texture and waviness always present on a real surface will alter the local angle of incidence across a beam of incident radiation. Smooth surfaces that behave like a mirror are referred to as specular reflectors. Otherwise, they form certain classes of diffuse reflectors.  A rough surface is defined as having a surface texture height variation greater than half the incident wavelength (λ).  Surface roughness is defined concerning wavelength and incidence angle.  Surfaces will appear to have a degree of roughness depending on which wavelength is imaged. When imaged, a surface will appear smooth if its average height variation is smaller than one-eighth of the wavelength. Therefore IR radiation (~1um) will be reflected more predictably by ~100nm rough surfaces (the reflected amount also depends on the material’s complex refractive index and absorption characteristics).  However, the same surface may appear rough and less predictable for the reflection intensity for imaging by blue light.  Or, within a visible spectrum, a surface will seem less rough in red light than when seen in green light.  A surface will also appear to be smooth as the incidence angle increases.  New results are beginning to indicate that nanofeature scattering happens strangely, increasing the reflectivity of smaller wavelengths of light as the features become smaller, thus producing unanticipated colors.  If the light is scattered back in the direction of incidence by a rough surface, it is referred to as backscattered light.  Many sensors are based on backscattered light, so for many images, rougher surfaces will appear brighter because of such sensors.

The color of a surface?  Thin Film Interference.

The reflection color from an object for sunlight depends on the intensity (including angle), polarization, photonic bandgap, refractive index (real and imaginary parts), and other properties such as roughness and multiscale nano periodicity (see the previous paragraph). The reflection or refraction of individual wavelengths may not be the same for all surfaces or thin films. Color separation often occurs just like in a prism but for different reasons. Butterfly wings have tiny scales covered with microscopic ridges and other structures. These play with light waves to create brilliant purple/blues and speckles of colors. Instead of a coloring chemical, the structure creates the concentration of wavelengths (color). They may also describe nano-scale texture. Such separation properties are also utilized for thin-film devices. Thin-film interference is a phenomenon associated with films that determine colors. The thin-film interference phenomena partially explain the colors of oxynitride and nitrided surfaces, tempered colors, and the color of butterflies’ wings! Thin films have many commercial applications, including partially transparent or anti-reflection coatings, mirrors, and optical filters.  For graded and compositionally variant films, the colors yield considerable important information about a coating or thin layer. The reflected, partly reflected, or refracted wave (depending on polarization) may interact and thus reveal information about the surface(s) from which individual frequency components are reflected, e.g., information about the film’s thickness or the film medium’s effective refractive index.  The reflection intensity depends on the refractive index,  extinction coefficient, and surface texture. 

The span of Visible Photon Energy with Color

Color Grating

Various colors of oxynitrides are often noted on a steel surface, as shown below.    These are called colors of tempering.  Amazingly these colors are also seen in cobalt and aluminum alloys and are not just for steels.    The color varies with the type of metal, time of film formation, phases, atmosphere/thickness, incident light distribution, and other surface textures.  Note specular and matte finishes below are possible for the common variations noted on iron and steel surfaces.

Why do these colors form on nano-surfaces?   From thin-film interference and back-scattered as well as diffuse-reflectance variations.

A surface appears smooth to the eye when the roughness is about a half to eight of the measurement wavelength, i.e., less than 500 nm (midpoint) for visible radiation) and when viewed at a high angle of incidence. Such surfaces can appear colored bluish when the auto-correlation length is small and the mean asperity roughnesses are very small at these texture levels. However, the surface constituents (phases) effects described below often dominate. The colors of titanium, zirconium, and alloy oxynitrides vary from red-yellow to blue/violet, indicating variations in the material’s bandgap that are enabled by oxygen/nitrogen ratio changes.  Texture compositing can create many colors when different phases coexist at a surface.  Thin-film interference, absorption coefficients, and internal scattering by small-scale phases like Fe2(CN) play a role in color formation. There is some analogy with the prism light grating shown above. However, the closest scientific analogy to the tempering colors of oxides and nitrides is noted in water-droplet residual drying colors on a surface, the colorful wings of an attractive butterfly (morpho-color), the spectacular color separation obtained from a prism-light grating, the red-shift explanation from moving objects, and the commonly observed variations in the color of the sky and across moonbows and rainbows.  However, very few clear explanations comprehensively explain all oxynitride surface colors.  Reflection, polarization, and a complex refractive index with a real part close to 1.55 seem important, but much more is to be learned about multi-scale roughness.  Hairy bird colors.  This roughness causes interference, but it’s caused by the minute surface structure of the skin or feathers of the bird, butterfly, beetle, or other creature we’re looking at. Incoming waves are reflected from different surface parts by nano-roughness in different amounts, which produces the amazing colors we see in nature by iridescence.

More on Spectral Radiance…

What is GoldenBlue®, and what does it have to do with solar devices?  Did you know that the Cascade e-ion could create photocatalytic or solar conversion surfaces?   Please contact MHI to learn more about surface quantum dots.

.    

Product Questions? Please Contact Us.

What is Deburr?  How does the Cascade e-ion change the surface roughness?  Does it impact the color of the surface?