Properties of Common Gases/Steam and Moist Air with Temperature
The Specific-Heat Capacity, C, is the heat required to raise the temperature by 1K per mole or kg. The SI unit of specific heat capacity is joule per kelvin per gram, J⋅g−1⋅K−1 (or kJ⋅kg−1⋅K−1 ),
The Specific Heat Capacity (specific heat) is typically measured and reported at constant Pressure (Cp) or constant volume (Cv).
These two values are almost the same for condensed matter (liquids or solids) because the condensed matter is almost incompressible. The heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules, i.e., the specific heat capacity of water is 4184 J⋅kg−1⋅K−1. This is only a general statement valid at atmospheric pressures.
For gases, the Cp and Cv have different values because gases are compressible.
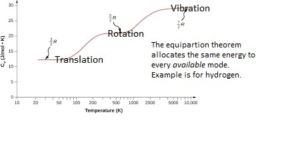
The specific heat reflects the energy taken up by translational (kinetic), rotational, and vibrational modes. Only the low-frequency modes, such as translational and rotational, can absorb energy (heat) at lower temperatures. The specific heats in units of J/mol.K are related to Ru, the Universal Gas Constant- Ru= 8.314 J/mol.K (0.0831 bar dm3 mol-1 K-1) for simple monoatomic gases. For monoatomic gases, Cp=2.5Ru, and Cv=1.5Ru, J/mol.K, respectively. The ratio of the two specific heats is called the adiabatic ratio of the gas. The symbol for the adiabatic ratio is g (gamma) and is equal to 1.667 for all monoatomic ideal gases like He, Ar, and Ne. Unless exceeding 10 Bar, most process gases can be treated as ideal, meaning that individual molecules and atoms do not feel any significant bond energy from other molecules or atoms in the same gas.
The specific heat changes, as shown below, with the number of atoms in a gas molecule. For diatomic gases, the Cp, Cv, and g are 3.5Ru, 2.5Ru, and 1.4, respectively. So far, we have only assumed that the gases are at a low temperature where the vibrational mode has not yet been accessed. Note that the energy distribution to the various rotational modes in diatomic gas has added 0.5Ru per mode to the gas-specific heat capacity over the monoatomic gas where rotational and vibrational modes are absent. This is a consequence of the equipartition theorem. A vibrational mode contributes twice as much to the heat capacity as a translational mode, but only if it is accessible. When vibrational modes are included, e.g., in a solid, the calculation of specific heat is not straightforward because the vibration frequencies (vibrionic modes) could span a range in a solid.
For condensed matter, the experimental heat capacity approaches a limit of 3Ru= 24.9 J/mol.K for simple substances like face-centered cubic metallic materials. For molecular or ordered solids, it will be more, e.g., ~ 6Ru= 49.884 J/mol.K, for dimolecular solids. When this happens, one may infer that all the vibrational mode possibilities are active (for absorbing energy). For solids and liquids, the two specific heats (Cp and Cv) are almost equal (aluminum is 24.2 J/mol.K, titanium is 26 J/mol.K, and Iron is 25.1 J/mol.K).
For ideal gases, the specific heat of the gas is independent of temperature. Specific heat values measured or calculated for polyatomic atomic configurations are temperature-dependent. The evidence regarding the behavior of vibrational energy in periodic (orderly) solids is that the collective vibrational modes can accept energy only in discrete amounts, and these energy quanta are labeled phonons (lattice vibration states). Like the photons of electromagnetic energy, the phonons obey Bose-Einstein statistics. At very low temperatures, only the specific contributions from electrons are essential, so the Fermi Dirac statistics apply. As an approximation, the dependence of the specific heat with temperature in Kelvin is T^3 (for the condensed matter) at low temperatures. The specific heat dependence is linear at higher temperatures before reaching a limit when all the vibrational states are fully active (without further dependence on temperature). If a phase change should occur, the specific heat is not defined at the phase change temperature. The heat capacity for steam at 100°C is 27.5 J/mol/K, which is about 3.3 R – until you get to T=700°C, where it rises to 3.5 R, and then at 1000°C, it is almost 4.0 R. In the case of a molecule like water, there are several degrees of freedom associated with different types of stretching and bending
Take me to the Airtorch® Models Page Take me to the Steam Generator Models Page.
![]()
Cp= Cv+Ru. Ru is 8.314 J/mol.K (universal constant) for all substances when expressed in the units J/mol.K. However, when expressed in kJ/kg.K units, the material-specific gas constant R depends on the materials. R equals Ru/M, where M is the molecular weight in moles/kg. Note that vibrational modes can be one to several depending on the molecule. Diatomic molecules can have stretching and bending modes. Note that hydrogen behaves more like a monoatomic gas at low temperatures.
R, the gas constant expressed in units of kJ/kg.K for common gases is given below.
Air 0.2870 kJ/kg.K
Hydrogen 4.1240 kJ/kg.K
Argon 0.2081 kJ/kg.K
Nitrogen 0.2986 kJ/kg.K
Oxygen 0.2598 kJ/kg.K
Steam 0.4615 kJ/kg.K
Most process gases are ideal at high temperatures and one atmospheric Pressure. The gas-specific heat capacity @ 300K is given below in the units kJ/kg. K. All the gases below are considered to be dry. If the gas is truly ideal, the specific heat capacity is temperature-independent.
Air Cp= 1.005 kJ/kg.K Cv=0.718 kJ/kg.K Density @ STP 1.29kg/m3
Hydrogen Cp=14.307 kJ/kg.K Cv=10.183 kJ/kg.K Density @ STP 0.09kg/m3
Argon Cp=0.5203 kJ/kg.K Cv=0.3122 kJ/kg.K Density @ STP 1.78kg/m3
CO2 Cp=0.8443 kJ/kg.K Cv=0.6553 kJ/kg.K Density @ STP 1.96kg/m3
Nitrogen Cp=1.0396 kJ/kg.K Cv=0.743 kJ/kg.K Density @ STP 1.25kg/m3
Oxygen Cp=0.918 kJ/kg.K Cv=0.658 kJ/kg.K Density @ STP 1.43kg/m3
Steam Cp=1.8723 kJ/kg.K Cv=1.4108 kJ/kg.K – see steam tables. (Steam has a strong temperature dependency for its specific heat)
At IUPAC standard temperature and pressure (0 °C and 101.325 kPa), dry air has a density of 1.2754 kg/m3. At 20 °C and 101.325 kPa, dry air has a density of 1.2041 kg/m3, i.e., at 70 °F and 14.696 psia, dry air has a density of 0.074887lbm/ft3.
Both energy and Enthalpy are measured from a base temperature. Therefore, only a change in properties of this kind is measurable. The difference in Enthalpy (H) is DH = Mass. Cp. (Change in temperature in Kelvin). The Internal Energy per kg (or specific internal energy) is given the symbol u. The Enthalpy per kg (or specific Enthalpy) is shown in the symbol h. The change in internal energy (U) is DU = Mass. Cv. (Change in temperature in Kelvin).
The table below gives Enthalpy per kg (h), Energy per kg (u), and Density of Air at various temperatures achieved by the Airtorch™. Base ~ 0K.
| Temperature of Air in Centigrade (°C). For Density, Enthalpy, and Energy, use a base of 0K. | Change in Enthalpy | Change in Internal Energy | Density Kg/m3 at a corresponding temperature in Centigrade (°C) given in THE first column |
|---|---|---|---|
200 | 200 | 143 | 0.7459 |
300 | 300 | 214 | 0.6158 |
400 | 401 | 286 | 0.5243 |
500 | 503 | 359 | 0.4565 |
600 | 607 | 435 | 0.4042 |
700 | 713 | 512 | 0.3627 |
800 | 822 | 592 | 0.3289 |
900 | 933 | 675 | 0.3008 |
1000 | 1046 | 759 | 0.2772 |
1500 | 1636 | 1205 | 0.1553 |
Please note that the above approximations should be verified from standard texts before use. Unintended typographical errors are possible.
Other Important Fluid Properties
Other important properties of a gas are dynamic Viscosity (defined below), kinematic Viscosity, and Prandtl number (defined below). For an ideal gas, these are independent of temperature. The Prandtl Number is often used in heat transfer and free and forced convection calculations. It depends on the fluid properties. The Pr ranges from 0.7 to 1.0 for standard process gasses, and Pr ranges from 0.001 to 0.03 for simple liquid metals. For polar liquids like water and oils, the Pr ranges from 1 – 2200 (the lower end for water and the higher for high molecular weight viscous oils). The Prandtl Number is a dimensionless number that is the ratio of momentum diffusivity (kinematic Viscosity) and thermal diffusivity. This number may, as you imagine, give a sense of comparison of viscous and thermal forces required for an objective and indicate what carries shear force to what carrier the thermal (heat) transport in a molecular sense!
Pr = v / α or Pr = μ cp / k where;
cp= specific heat capacity (J/kg K) at constant pressure,
k = thermal conductivity (W/m K)
μ = absolute or dynamic Viscosity (kg/ms). The dynamic ( or absolute) Viscosity is the tangential force per unit area required to move one horizontal plane of a fluid concerning the other at unit velocity when maintained a unit distance apart.
α = thermal diffusivity (m2/s)
v = kinematic viscosity or momentum diffusivity (m2/s). Kinematic Viscosity is the ratio of absolute or dynamic Viscosity to density. Kinematic Viscosity can be obtained by dividing the absolute Viscosity of a fluid by density.
Pr = Prandtl’s number. (Note dimensionless).
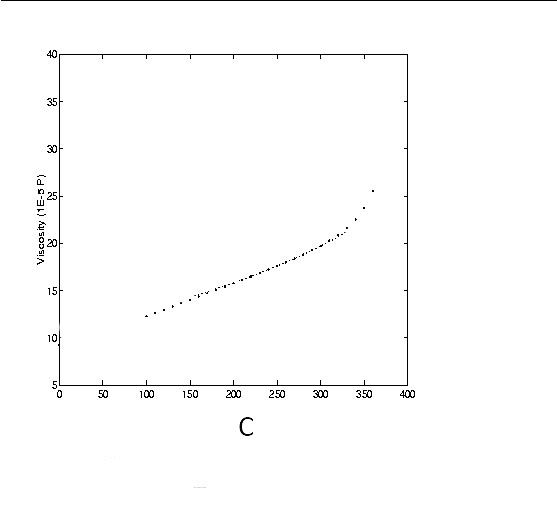
Viscosity of Steam
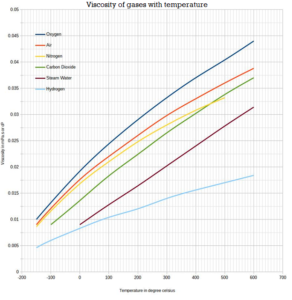 The Viscosity of gases with temperature
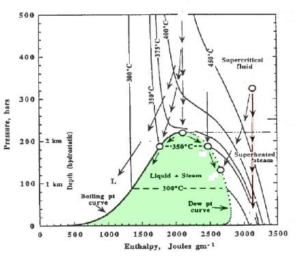
Pressure Enthalpy Diagram for Water-Steam |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Water vapor pressure
The water vapor exerts Pressure on the walls of the container. In a closed container partly filled with water, water vapor will be in the space above the water. The concentration of water vapor depends only on the temperature. It is not dependent on the amount of water and is only slightly influenced by the air pressure in the container. The empirical equations below give a good approximation to the saturation water vapor pressure at temperatures within the limits of the earth’s climate.
Saturation vapor pressure (svp), ps, in pascals:
ps = 610.78 *exp( t / ( t + 238.3 ) *17.2694 )
where t is the temperature in degrees Celsius
The svp below freezing can be corrected after using the equation above, thus:
ps ice = -4.86 + 0.855*ps + 0.000244*ps2
The next formula gives a direct result for the saturation vapor pressure over ice:
ps ice = exp( -6140.4 / ( 273 + t ) + 28.916 )
Pascal is the SI unit of Pressure = newtons / m2. Atmospheric Pressure is about 100,000 Pa (standard atmospheric Pressure is defined as 101,300 Pa).
Water vapor concentration
The relationship between vapor pressure and concentration is defined for any gas by the equation:
p = nRT/V
p is the Pressure in Pa, V is the volume in cubic meters, T is the temperature in degrees Kelvin (degrees Celsius + 273.16), n is the quantity of gas expressed in molar Mass ( 0.018 kg in the case of water ), R is the gas constant: 8.31 Joules/mol.K
To convert the water vapor pressure to concentration in kg/m3: ( Kg / 0.018 ) / V = p / RT
kg/m3 = 0.002166 *p / ( t + 273.16 ) where p is the actual vapor pressure
Relative Humidity
Relative Humidity (RH) is the ratio of the actual water vapor pressure to the saturation water vapor pressure at the prevailing temperature.
RH = p/ps
RH is usually expressed as a percentage rather than as a fraction.
The RH is a ratio. It does not define the water content of the air unless the temperature is given. RH is so much used in conservation because most organic materials have an equilibrium water content that is mainly determined by the RH and is only slightly influenced by temperature.
Notice that air is not involved in the definition of RH. Air is the transporter of water vapor in the atmosphere and air conditioning systems, so the phrase “RH of the air” is commonly used and occasionally misleading. Airless space can have an RH. The independence of RH from atmospheric Pressure is not important on the ground. Still, it does have some relevance to calculations concerning the air transport of works of art and conservation by freeze-drying.
The Dew Point
The water vapor content of air is often quoted as a dew point. This is the temperature to which the air must be cooled before dew condenses. At this temperature, the actual water vapor content of the air is equal to the saturation water vapor pressure. The dew point is usually calculated from the RH. The first one calculates ps, the saturation vapor pressure at the ambient temperature. The actual water vapor pressure, pa, is:
pa= ps * RH% / 100
The next step is calculating the temperature at which pa would be the saturation vapor pressure. This means running backward the equation given above for deriving saturation vapor pressure from temperature:
Let w = ln ( pa/ 610.78 )
Dew point = w *238.3 / ( 17.294 – w )
This calculation is often used to judge the probability of condensation on windows and within walls and roofs of humidified buildings.
The dew point can also be measured directly by cooling a mirror until it fogs. The following ratio then gives the RH.
RH = 100 * ps dewpoint/ps ambient
The concentration of water vapor in the air
It is sometimes convenient to quote water vapor concentration as kg/kg of dry air. This is used in air conditioning calculations and is mentioned on psychrometric charts. The following calculations for water vapor concentration in air apply at ground level.
Dry air has a molar mass of 0.029 kg. It is denser than water vapor, with a molar mass of 0.018 kg. Therefore, humid air is lighter than dry air. If the total atmospheric Pressure is P and the water vapor pressure is p, the partial pressure of the dry air component is P – p. The weight ratio of the two components, water vapor, and dry air, is:
kg water vapor / kg dry air = 0.018 *p / ( 0.029 *(P – p ) )
= 0.62 *p / (P – p )
At room temperature, P – p is nearly equal to P, which at ground level is close to 100,000 Pa, so approximately:
kg water vapor / kg dry air = 0.62 *10-5 *p
Thermal properties of damp air
Heat transfer control can be used to control the drying and wetting of materials during conservation treatment. The transfer of heat from an air stream to a wet surface, which releases water vapor to the airstream at the same time as it cools it, is the basis for psychrometry and many other microclimatic phenomena. The heat content, usually called the Enthalpy of the air, rises with increasing water content. This hidden heat, called latent heat by air conditioning engineers, has to be supplied or removed to change the relative humidity of the air, even at a constant temperature. This is relevant to conservators.
The Enthalpy of dry air is not known. Air at zero degrees Celsius is defined as having zero enthalpies. The Enthalpy, in kJ/kg, at any temperature, t, between 0 and 60C is approximate:
h = 1.007t – 0.026 below zero: h = 1.005t
The Enthalpy of liquid water is sometimes defined as zero at zero degrees Celsius. Turning liquid water to vapor at the same temperature requires considerable heat energy: 2501 kJ/kg at 0C.
At temperature t, the heat content of water vapor is:
hw = 2501 + 1.84t
Notice that water vapor, once generated, also requires more heat than dry air to raise its temperature further: 1.84 kJ/kg.C against about one kJ/kg.C for dry air.
The Enthalpy of moist air, in kJ/kg, is, therefore:
h = (1.007*t – 0.026) + g*(2501 + 1.84*t)
g is the water content (specific humidity) in kg/kg of dry air
The Psychrometer
The final formula in this collection is the psychrometric equation. The psychrometer is the nearest to an absolute method of measuring RH that the conservator ever needs. It is more reliable than electronic devices because it depends on the calibration of thermometers or temperature sensors, which are much more reliable than electrical RH sensors. The only limitation of the psychrometer is that it is difficult to use in confined spaces (not because it needs to be whirled around but because it releases water vapor).
The psychrometer, or wet and dry bulb thermometer, responds to the RH of the air in this way:
Unsaturated air evaporates water from the wet wick. The heat required to evaporate the water into the air stream is taken from it, which cools in contact with the wet surface, thus cooling the thermometer beneath it. An equilibrium wet surface temperature is reached, roughly halfway between ambient and dew point temperatures.
The air’s potential to absorb water is proportional to the difference between the mole fraction, ma, of water vapor in the ambient air and the mole fraction, mw, of water vapor in the saturated air at the wet surface. It is this capacity to carry away water vapor that drives the temperature down to, tw, the wet thermometer temperature, from the ambient temperature ta :
(mw – ma) = B(ta- tw)
B is a constant whose numerical value can be derived theoretically by some rather complicated physics (see the reference below).
The water vapor concentration is expressed here as a mole fraction in the air rather than as vapor pressure. Air is involved in the psychrometric equation because it brings the heat required to evaporate water from the wet surface. Therefore, the constant B depends on total air pressure, P. However, the mole fraction, m, is simply the ratio of vapor pressure p to total pressure P: p/P. The air pressure is the same for both ambient air and air in contact with the wet surface, so the constant B can be modified to a new value, A, which incorporates the Pressure, allowing the molar fractions to be replaced by the corresponding vapor pressures:
pw – pa= A* ( ta- tw)
The relative humidity (as already defined) is the ratio of pa, the actual water vapor pressure of the air, tops, and the saturation water vapor pressure at ambient temperature.
RH% = 100 *pa/ ps = 100 *( pw – ( ta- tw) * 63) / ps
When the wet thermometer is frozen, the constant changes to 56
The psychrometric constant is taken from: R.G.Wylie & T. Lalas, “Accurate psychrometer coefficients for wet and ice-covered cylinders in laminar transverse air streams,” in Moisture and Humidity 1985, published by the Instrument Society of America, pp 37 – 56. These values are slightly lower than those in general use. There are tables and slide rules for calculating RH from the psychrometer, but a programmable calculator is convenient. Alternatively, click on the calculator.
| Properties of Various Gases (at 300 K) that are close to ideal (i.e., close to the specific heat ratio k-1.667) | ||||||
| Gas | Molecular Formula | Molar Mass | Gas constant | Specific Heat at Constant Pressure, Cp. | Specific Heat at Constant Volume Cv | Specific Heat Ratio |
| Units | M[kg/kmol] | R[kJ/kg.K] | Cp[kJ/kg.K] | Cv[kJ/kg.K] | k = Cp/Cv | |
| Air | Typical | 28.97 | 0.287 | 1.005 | 0.718 | 1.4 |
| Argon | Ar | 39.948 | 0.2081 | 0.5203 | 0.3122 | 1.667 |
| Butane | C4H10 | 58.124 | 0.1433 | 1.7164 | 1.5734 | 1.091 |
| Carbon Dioxide | CO2 | 44.01 | 0.1889 | 0.846 | 0.657 | 1.289 |
| Carbon Monoxide | CO | 28.011 | 0.2968 | 1.04 | 0.744 | 1.4 |
| Ethane | C2H6 | 30.07 | 0.2765 | 1.7662 | 1.4897 | 1.186 |
| Ethylene | C2H4 | 28.054 | 0.2964 | 1.5482 | 1.2518 | 1.237 |
| Helium | He | 4.003 | 2.0769 | 5.1926 | 3.1156 | 1.667 |
| Hydrogen | H2 | 2.016 | 4.124 | 14.307 | 10.183 | 1.405 |
| Methane | CH4 | 16.043 | 0.5182 | 2.2537 | 1.7354 | 1.299 |
| Neon | Ne | 20.183 | 0.4119 | 1.0299 | 0.6179 | 1.667 |
| Nitrogen | N2 | 28.013 | 0.2968 | 1.039 | 0.743 | 1.4 |
| Octane | C8H18 | 114.231 | 0.0729 | 1.7113 | 1.6385 | 1.044 |
| Oxygen | O2 | 31.999 | 0.2598 | 0.918 | 0.658 | 1.395 |
| Propane | C3H8 | 44.097 | 0.1885 | 1.6794 | 1.4909 | 1.126 |
| Steam | H2O | 18.015 | 0.4615 | 1.8723 | 1.4108 | 1.327 |
Heat Values of Various Fuels
A fuel’s “heat value,” or energy or calorific value, is the heat released during combustion. The heat value measures a fuel’s energy density and is expressed in energy (joules) per specified amount (kilograms, kg).
| Fuel | Heat value |
| Hydrogen (H2) | 120-142 MJ/kg |
| Methane (CH4) | 50-55 MJ/kg |
| Methanol (CH3OH) | 22.7 MJ/kg |
| Propane (C3H8) | 46 MJ/kg |
| Dimethyl ether – DME (CH3OCH3) | 29 MJ/kg |
| Petrol/gasoline | 44-46 MJ/kg |
| Diesel fuel | 42-46 MJ/kg |
| Crude oil | 42-47 MJ/kg |
| Liquefied petroleum gas (LPG) | 46-51 MJ/kg |
| Natural gas | 42-55 MJ/kg |
| Hard black coal (IEA definition) | >~23.9 MJ/kg |
| Hard black coal (Australia & Canada) | c. 25 MJ/kg |
| Sub-bituminous coal (IEA definition) | 17.4-23.9 MJ/kg |
| Sub-bituminous coal (Australia & Canada) | c. 18 MJ/kg |
| Lignite/brown coal (IEA definition) | <17.4 MJ/kg |
| Lignite/brown coal (Australia, electricity) | c. 10 MJ/kg |
| Firewood (dry) | 16 MJ/kg |
| Natural uranium in LWR (normal reactor) | 500 GJ/kg |
| Natural uranium, in LWR with U & Pu, recycle | 650 GJ/kg |
| Natural uranium, in FNR | 28,000 GJ/kg |
| Uranium enriched to 3.5% in LWR | 3900 GJ/kg |
Uranium figures are based on 45,000 MWd/t burn-up of 3.5% enriched U in LWR
MJ = 106 Joule, GJ = 109 J
One tonne of oil equivalent is equal to 41.868 GJ
MightySteam® Products (Industrial and R&D Use)
MigthySteam® Controlled Humidity Products (Commercial Use)
Use less energy for the same outcome.
Energy savings with steam for deep decarbonization.
Oxygen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Modern PLC, SCR, HMI (touch screen) operation. Remote communications and control. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nitrogen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Argon | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Carbon dioxide | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
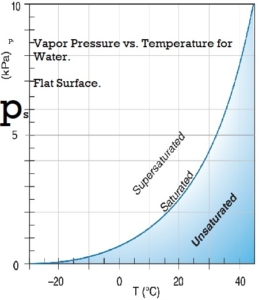
Water vapor pressure
The water vapor exerts pressure on the walls of the container. In a closed container partly filled with water, water vapor will be in the space above the water. The concentration of water vapor depends only on the temperature. It is not dependent on the amount of water and is only slightly influenced by the air pressure in the container. The empirical equations below give a good approximation to the saturation water vapor pressure at temperatures within the limits of the earth’s climate.
Saturation vapor pressure, ps, in pascals:
ps = 610.94 *exp(( T*17.6294) / ( T + 243 ) )
where T is the temperature in degrees Celsius
The svp below freezing can be corrected after using the equation above, thus:
ps ice = -4.86 + 0.855*ps + 0.000244*ps2
The next formula gives a direct result for the saturation vapor pressure over ice:
ps ice = 611.2 exp( 22.587*T / ( T+273)
The Pascal is the SI unit of pressure = newtons / m2. Atmospheric pressure is about 100,000 Pa (standard atmospheric pressure is 101,300 Pa).
Water vapor concentration
The relationship between vapor pressure and concentration is defined for any gas by the equation:
p = nRT/V
p is the pressure in Pa, V is the volume in cubic meters, T is the temperature (degrees Celsius + 273.16), n is the quantity of gas expressed in molar mass ( 0.018 kg in the case of water ), R is the gas constant: 8.31 Joules/mol.K
To convert the water vapor pressure to concentration in kg/m3: ( Kg / 0.018 ) / V = p / RT
kg/m3 = 0.002166 *p / ( T+ 273.16 ) where p is the actual vapor pressure
Relative Humidity
Relative Humidity (RH) is the ratio of the actual water vapor pressure to the saturation water vapor pressure at the prevailing temperature.
RH = p/ps
RH is usually expressed as a percentage rather than as a fraction.
The RH is a ratio. It does not define the water content of the air unless the temperature is given. RH is so much used in conservation because most organic materials have an equilibrium water content mainly determined by the RH and are only slightly influenced by temperature.
Notice that air is not involved in the definition of RH. Air is the transporter of water vapor in the atmosphere and air conditioning systems, so “RH of the air” is commonly used and occasionally misleading. Airless space can have an RH. The independence of RH from atmospheric pressure is not important on the ground. Still, it does have some relevance to calculations concerning the air transport of works of art and conservation by freeze-drying.
The Dew Point
The water vapor content of air is often quoted as a dew point. This is the temperature to which the air must be cooled before dew condenses. At this temperature, the actual water vapor content of the air is equal to the saturation water vapor pressure. The dew point is usually calculated from the RH. The first one calculates ps, the saturation vapor pressure at the ambient temperature. The actual water vapor pressure, pa, is:
pa= ps * RH% / 100
The next step is calculating the temperature at which pa would be the saturation vapor pressure. This means running backward the equation given above for deriving saturation vapor pressure from temperature:
Let w = ln ( pa/ 610.78 )
Dew point = w *238.3 / ( 17.294 – w )
This calculation is often used to judge the probability of condensation on windows and within walls and roofs of humidified buildings.
The dew point can also be measured directly by cooling a mirror until it fogs. The ratio then gives the RH.
RH = 100 * ps (dewpoint)/ps (ambient)
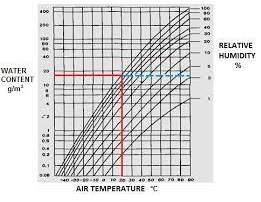
The concentration of water vapor in the air
It is sometimes convenient to quote water vapor concentration as kg/kg of dry air. This is used in air conditioning calculations and is quoted on psychrometric charts. The following calculations for water vapor concentration in air apply at ground level.
Dry air has a molar mass of 0.029 kg. It is denser than water vapor, with a molar mass of 0.018 kg. Therefore, humid air is lighter than dry air. If the total atmospheric pressure is P and the water vapor pressure is p, the partial pressure of the dry air component is P – p. The weight ratio of the two components, water vapor, and dry air, is:
kg water vapor / kg dry air = 0.018 *p / ( 0.029 *(P – p ) )
= 0.62 *p / (P – p )
At room temperature, P – p is nearly equal to P, which at ground level is close to 100,000 Pa, so approximately:
kg water vapor / kg dry air = 0.62 *10-5 *p
Thermal properties of damp air
Heat transfer control can control the drying and wetting of materials during conservation treatment. The transfer of heat from an air stream to a wet surface, which releases water vapor to the airstream at the same time as it cools it, is the basis for psychrometry and many other microclimatic phenomena. The heat content, usually called the enthalpy of the air, rises with increasing water content. This hidden heat, called latent heat by air conditioning engineers, has to be supplied or removed to change the relative humidity of the air, even at a constant temperature. This is relevant to conservators.
Air at zero degrees Celsius is defined as having zero enthalpies. The enthalpy, h, in kJ/kg, at any temperature, T (K), between 0 and 60°C is approximately:
h = 1.007T – 0.026, below zero: h = 1.005T
Liquid water’s enthalpy is sometimes defined as zero at zero degrees Celsius. Turning liquid water to vapor at the same temperature requires a considerable amount of heat energy: ~2501 kJ/kg at 0C.
At a temperature T, the heat content of water vapor is:
hw = 2501 + 1.84T
Notice that water vapor, once generated, also requires more heat than dry air to raise its temperature further: 1.84 kJ/kg.K against about one kJ/kg.K for dry air.
The enthalpy of moist air, in kJ/kg, is, therefore:
h = (1.007*T – 0.026) + g*(2501 + 1.84*T)
g is the water content (specific humidity) in kg/kg of dry air
The Psychrometer
The final formula in this collection is the psychrometric equation. The psychrometer is the nearest to an absolute method of measuring RH that the conservator ever needs. It is more reliable than electronic devices because it depends on the calibration of thermometers or temperature sensors, which are much more reliable than electrical RH sensors. The only limitation of the psychrometer is that it is difficult to use in confined spaces (not because it needs to be whirled around but because it releases water vapor).
The psychrometer, or wet and dry bulb thermometer, responds to the RH of the air in this way:
Unsaturated air evaporates water from the wet wick. The heat required to evaporate the water into the air stream is taken from it, which cools in contact with the wet surface, thus cooling the thermometer beneath it. An equilibrium wet surface temperature is reached, roughly halfway between ambient and dew point temperatures.
The air’s potential to absorb water is proportional to the difference between the mole fraction, ma, of water vapor in the ambient air and the mole fraction, MW, of water vapor in the saturated air at the wet surface. It is this capacity to carry away water vapor that drives the temperature down to, Tw, the wet thermometer temperature, from the ambient temperature ta :
(mw – ma) = B(Ta- Tw)
B is a constant whose numerical value can be derived theoretically by some rather complicated physics.
The water vapor concentration is expressed here as a mole fraction in the air rather than as vapor pressure. Air is involved in the psychrometric equation because it brings the heat required to evaporate water from the wet surface. Therefore, the constant B depends on total air pressure, P. However, the mole fraction, m, is simply the ratio of vapor pressure p to total pressure P: p/P. The air pressure is the same for both ambient air and air in contact with the wet surface, so the constant B can be modified to a new value, A, which incorporates the pressure, allowing the molar fractions to be replaced by the corresponding vapor pressures:
pw – pa= A* ( Ta- Tw)
The relative humidity (as already defined) is the ratio of pa, the actual water vapor pressure of the air, tops, and the saturation water vapor pressure at ambient temperature.
RH% = 100 *pa/ ps = 100 *( pw – ( Ta- Tw) * 63) / ps
When the wet thermometer is frozen, the constant changes to 56
The psychrometric constant is taken from: R.G.Wylie & T. Lalas, “Accurate psychrometer coefficients for wet and ice-covered cylinders in laminar transverse air streams,” in Moisture and Humidity 1985, published by the Instrument Society of America, pp 37 – 56. These values are slightly lower than those in general use. There are tables and slide rules for calculating RH from the psychrometer, but a programmable calculator is convenient. Alternatively, click on the calculator.
Relative Humidity Chart
Material Resistivity ρ (Ω•m) at 20 °C Conductivity σ (S/m) at 20 °C
Silver 1.59×10−8 6.30×107
Copper 1.68×10−8 5.96×107
Cu- Ni Wire 1.7×10-8 5.95 x107
Annealed copper 1.72×10−8 5.80×107
Gold 2.44×10−8 4.10×107
Aluminum 2.82×10−8 3.5×107
Tin 1.09×10−7 9.17×106